Probabilistic Hierarchical Clustering In Data Mining

In the world of data science, clustering is a popular technique used to group similar objects or data points together. One of the most commonly used clustering methods is hierarchical clustering, which involves creating a tree-like structure that represents how different clusters are related to each other. However, traditional hierarchical clustering has some limitations when it comes to dealing with uncertainty and noise in the data. This is where probabilistic hierarchical clustering comes into play. For an in-depth understanding of probabilistic hierarchical clustering, our data scientist course online helps you explore more about hierarchical clustering and data mining, the most effective tool of data science.

What is Hierarchical Clustering?

Hierarchical clustering is a method of grouping similar objects or data points together based on their similarity/dissimilarity measures. It involves creating a tree-like structure called a dendrogram that shows how different clusters are related to each other. The two main types of hierarchical clustering are agglomerative (bottom-up) and divisive (top-down). In agglomerative hierarchical clustering, each object starts as its cluster, and then pairs of clusters are merged until all objects belong to one big cluster at the top level. Divisive hierarchical clustering works in reverse by starting with one big cluster and recursively dividing it into smaller sub-clusters until every object belongs to its own individual cluster.

Limitations of Using Traditional Hierarchical Clustering

Traditional hierarchical clustering assumes that there is no uncertainty or noise in the data being clustered. However, this assumption does not hold for many real-world datasets where there may be missing values, outliers, or measurement errors present in the data. Traditional methods also assume that all features have equal importance, which may not always be true.

Probabilistic Hierarchical Clustering

Hierarchical clustering algorithms that use linkage metrics are typically the most successful and intelligible clustering algorithms. Their application in cluster analysis is quite common. Nevertheless, algorithmic hierarchical clustering approaches may give rise to several problems in certain circumstances. To get things started, selecting an appropriate distance measure for hierarchical clustering is not always a straightforward task. Second, to apply the algorithmic method, all of the data object attributes and their corresponding values need to be present. When just parts of the data are available, it is challenging to employ a hierarchical algorithmic clustering technique (i.e., certain attribute values of some objects are absent). Third, the majority of heuristic hierarchical clustering algorithms search the immediate area at each step for a feasible merging or splitting alternative. As a direct consequence of this, the optimization aim of the ensuing cluster hierarchy might not be immediately apparent.

Probabilistic hierarchical clustering attempts to compensate for some of these shortcomings by using probabilistic models to measure the distances between groups.One of the many perspectives from which the clustering problem can be analyzed is as a sample of the generative model, often known as the underlying data creation process. This is only one of the many possible approaches. When running a clustering analysis on the data, it is assumed that the replies to a collection of marketing surveys reflect a representative cross-section of all potential customers. This is done so that the results may be compared. In this particular instance, the data generator comprises a probability distribution.The dispersion of viewpoints about different customers, knowledge of which cannot be obtained coherently. The observed data items are utilized to arrive at an accurate approximation of the generative model through the process of clustering.

Distributions And Their Use In Probabilistic Hierarchical Clustering:

The Gaussian and Bernoulli distributions are two examples of common distribution functions that data generative models employ. Both of these distributions may be parameterized and are capable of being applied in practice. Because of this, the challenge of learning a generative model is reduced to one of finding which values of its parameters produce the highest fit with the data that we have available.

Having generative capabilities built into the model. Imagine that we have been given the task of doing cluster analysis on a set of one-dimensional points denoted by X = x1,...,xn. If we assume that a Gaussian distribution is to blame for the production of the data points,

where the parameters are µ (the mean) and σ 2 (the variance). The probability that the model then generates a point xi ∈ X is 

Consequently, the likelihood that the model generates X is

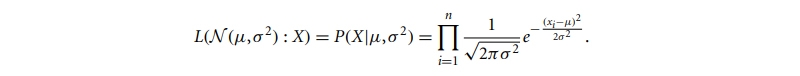
The aim of learning the generative model is to discover the parameters 2 such that the likelihood is maximized. Another way to say this is to say that the task of learning the generative model is to identify the parameters L(N (µ,σ 2 ): X).

N (µ0,σ 2 0 ) = argmax{L(N (µ,σ 2 ) : X)},

where max{L(N (µ,σ 2 ) : X)} is called the maximum likelihood. 

If you have a group of items, you may use maximum likelihood to determine how well they cluster together. The standard of an m-cluster (C1,..., Cm) divided collection of items is defined as

Q({C1,..., Cm}) = i=1mP(Ci),

where P() is the maximum likelihood. If we merge two clusters, Cj1 and Cj2, into a cluster, Cj1 ∪Cj2, then the change in the quality of the overall clustering is 

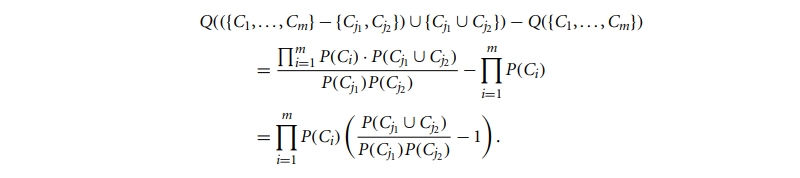
In hierarchical clustering, Qm i=1 P(Ci) is constant for each pair of clusters while deciding whether or not to merge them. As a result, the gap between clusters C1 and C2 may be calculated, given their coordinates.

dist(Ci, Cj) = −log P(C1 ∪C2)/ P(C1)P(C2) 

A probabilistic hierarchical clustering strategy may employ the agglomerative clustering framework, but probabilistic models will be used to determine the distance between groups.Examination in great detail of Eq. demonstrates that the quality of the clustering may not necessarily improve when two clusters are joined; more specifically, the probability that P(Cj1 Cj2) P(Cj1)P(Cj2) is greater than 1 may not always be the case. 

Probabilistic Hierarchical Clustering Using Gaussian Distribution

For illustration, let us assume that the model shown uses Gaussian distribution functions. Combining clusters C1 and C2 will have a cluster that more closely resembles a Gaussian distribution. On the other hand, if you combine clusters C3 and C4, you will obtain a less well-clusterable cluster because no Gaussian functions fit it well.

Based on this finding, if their distance is negative, a probabilistic hierarchical clustering technique can start with one cluster for each item and merge two clusters, Ci and Cj. During each iteration, the objective is to locate Ci and Cj in such a way that the logarithm of the product of P(CiCj) and P(Ci)P(Cj) is maximized. If the quality of the clustering increases with each iteration, as assessed by log P(CiCj) P(Ci)P(Cj) > 0, the iteration will continue. If the opposite is true, the iteration will stop. The pseudocode is included in an algo file that is given.

The performance of probabilistic hierarchical clustering methods is equivalent to that of algorithmic agglomerative hierarchical clustering methods, and these approaches are also significantly easier to understand than their algorithmic counterparts. Although probabilistic models are simpler to understand, they do not have the same degree of adaptability as distance measurements in certain contexts. Probabilistic models, as opposed to other types, can effectively manage data that can only be seen in part. When presented with a multidimensional data set, for example, in which some objects lack values on certain dimensions, it is possible to learn a Gaussian model on each dimension separately by making use of the observed values on the dimension. This can be done by utilizing the observed values on the dimension. We can achieve our optimization goal of fitting the data to the probabilistic models we have chosen by developing a hierarchical structure for the clusters we created.

The usage of probabilistic hierarchical clustering does have one significant drawback, however, and that is the fact that it only creates one hierarchy with respect to the chosen probabilistic model. This is a significant drawback. It is not enough for cluster hierarchies due to the inherent uncertainty that they bring about. There is a possibility that the data set can support many hierarchies, each of which

Merging clusters in probabilistic hierarchical clustering:

 (a) Merging clusters C1 and C2 leads to an increase in overall cluster quality, but merging clusters (b) C3 and (c) C4 does not.

Algorithm: A Probabilistic Hierarchical Clustering Algorithm

Input: D = {o1,..., on}: a data set containing n objects; 

Output: A hierarchy of clusters.

 Method:

1. Create a cluster for each object Ci = {oi}, 1 ≤ i ≤ n; 
2. For i = 1 to n
3. Find pair of clusters Ci and Cj such that Ci, Cj = argmaxi6=j log P(Ci∪Cj ) P(Ci )P(Cj ) ;
4. If log P(Ci∪Cj ) P(Ci )P(Cj ) > 0 then merge Ci and Cj ;
5. Else stop;

The distribution of such hierarchies cannot be determined using either algorithmic or probabilistic methods. These issues have recently inspired the development of Bayesian tree-structured models. Advanced subjects such as Bayesian and other complex probabilistic clustering algorithms are outside the scope of this book.

Advantages of Using Probabilistic Hierarchical Clustering

There are various advantages of using probabilistic hierarchical clustering over the traditional clustering algorithm: 

• One of the key advantages of probabilistic hierarchical clustering is its ability to handle complex and heterogeneous data sets that may contain noise or missing values. Traditional clustering algorithms often struggle with these types of datasets as they assume that all variables are equally important and have equal variance. In contrast, probabilistic hierarchical clustering can account for differences in variable importance by modeling them as probability distributions rather than fixed values. This allows the algorithm to identify clusters based on patterns across multiple dimensions rather than relying solely on one or two features.
• Another advantage of probabilistic hierarchical clustering is its ability to provide uncertainty estimates for each observation's cluster membership. Unlike traditional algorithms that assign each point to a single cluster with no indication of how confident it is in that assignment, this approach provides probabilities indicating how likely an object belongs in a particular group given the available evidence (i.e., other observations within the same cluster). These probabilities can be used to evaluate the reliability of individual clusters or compare different models' performance.
• Finally, probabilistic hierarchical clustering offers more flexibility when selecting appropriate models compared with traditional methods. Instead of assuming a specific number of groups (e.g., k-means), users can choose from various model structures, such as Gaussian mixture models (GMM) or Dirichlet process mixture models (DPMMs), depending on their data characteristics and research questions. For example, GMMs are useful when there are clear separations between groups but also some overlap between them; DPMMs work well when there might be an unknown number of latent subgroups within larger classes.

Drawbacks of Using Probablistic Hierarchical Clustering

Despite numerous advantages, there are other limitations of using probabilistic hierarchical clustering: 

• One of the main drawbacks of Probabilistic Hierarchical Clustering is its computational complexity. The algorithm involves computing probabilities for each data point and cluster at every level of the hierarchy, which can become time-consuming as the dataset grows. This can make it impractical for large-scale applications or real-time analysis where speed is essential.
• Another disadvantage of Probabilistic Hierarchical Clustering is its sensitivity to initialization parameters. The results produced by this method can vary significantly depending on how initial values are chosen for model parameters such as cluster centers and variances. As a result, selecting appropriate initial values becomes critical to obtaining accurate results.
• A further limitation of Probabilistic Hierarchical Clustering is its assumption of Gaussian distributions within clusters. This means that if your dataset contains non-Gaussian distributions or outliers, this method may not accurately identify those patterns within your data.
• Finally, interpreting the results obtained from Probabilistic Hierarchical Clustering requires domain knowledge and expertise in statistical modeling since there are no clear-cut rules defining what constitutes a good clustering solution versus one that does not fit well with existing knowledge about the problem being studied.

Applications of Using Probablistic Hierarchical Clustering

Probabilistic hierarchical clustering is a machine learning technique that groups similar data points into clusters. This method assigns probabilities to the likelihood of a point belonging to each cluster, allowing for more flexible and nuanced categorization than traditional clustering methods.

The applications of probabilistic hierarchical clustering are diverse and can be found in many fields, such as biology, finance, marketing, and computer science. Here are some examples:

1. Biology: In genomics research, probabilistic hierarchical clustering can be used to identify genes with similar expression patterns across different samples or conditions. This information can help researchers understand how different genes interact with each other in biological processes.
2. Finance: Probabilistic hierarchical clustering has been applied in portfolio optimization strategies by grouping stocks based on their risk-return profiles. By assigning probabilities to the membership of each stock in multiple clusters, investors can construct portfolios that balance risk and return while maximizing diversification.
3. Marketing: Clustering customers based on their purchasing behavior using probabilistic hierarchical clustering allows companies to target specific groups with tailored marketing campaigns or product offerings.
4. Computer Science: Probabilistic hierarchical clustering is also useful for image recognition tasks where images must be classified into categories based on visual features such as color and texture.
5. Social Sciences: Researchers use this method for text analysis by analyzing large volumes of textual data from social media platforms or online forums through topic modeling techniques like Latent Dirichlet Allocation (LDA), which uses probabilistic graphical models approach.

Data Science Training

• Personalized Free Consultation
• Access to Our Learning Management System
• Access to Our Course Curriculum
• Be a Part of Our Free Demo Class

Sign Up Now

Conclusion

Probabilistic hierarchical clustering offers an improved approach to traditional hierarchical clustering by incorporating probabilistic models into the dendrogram-building process. Allowing for partial membership probabilities between clusters provides greater flexibility when dealing with uncertainty and noise in real-world datasets. Its advantages have made it increasingly popular among researchers working on complex datasets across various fields, including biology, computer science, finance, etc. Understanding probabilistic hierarchical clustering in data mining begins with understanding data science; you can get an insight into the same through our professional certification courses.