Understanding Different Types of Distance Measures in Machine Learning

Distance measures are crucial in machine learning algorithms, especially in clustering. Clustering is the process of grouping similar data points together based on certain criteria. In order to perform this task effectively, different types of distance measures are used to calculate the similarity or dissimilarity between data points. Let's dive more into the topic of distance measures in algorithm methods and learn more about their importance in data science and key takeaways. You should check out the data science tutorial guide to clarify your basic concepts. 

In this blog post, we will discuss various distance measures that are commonly used in machine learning and their significance in clustering algorithms.

What are Distance Measures?

The distance measure is a mathematical concept that calculates the similarity or dissimilarity between two objects. It is an essential component of many machine learning algorithms as it helps us understand how close or far apart different data points are from each other.

Several types of distance measures are available such as Euclidean distance, Manhattan distance, Minkowski distance, Cosine Similarity, and Jaccard Similarity, among others. 

Types of Clustering Distance Measures

Clustering is one of the most popular unsupervised machine learning techniques involving grouping similar data points into clusters. The aim here is to find patterns within unlabelled datasets without prior knowledge.

To achieve this goal, clustering algorithms use various distance measures to calculate similarities between data points. Some common examples include:

The Euclidean Distance 

The Euclidean distance measure is a commonly used method for measuring the similarity or dissimilarity between two data points in n-dimensional space. It is based on the Pythagorean theorem, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of its other two sides.

In practice, this means that to calculate the Euclidean distance between two data points (x1, y1) and (x2, y2), we simply need to take their differences in each dimension (i.e., x2 - x1 and y2 - y1), square them, add them together, and then take the square root of this sum. In mathematical notation:

d(x,y) = sqrt((x2-x1)^2 + (y2-y1)^2)

This formula can be extended to any number of dimensions by adding additional terms inside the square root for each dimension.

One important consideration when using Euclidean distance measure is that it works best with continuous variables. For example, if we compare two people based on their height and weight, both variables are continuous and can be easily measured as numeric values. However, if we were comparing people based on their favorite color or political affiliation, these variables would be categorical and unsuitable for Euclidean distance use.

The Manhattan Distance 

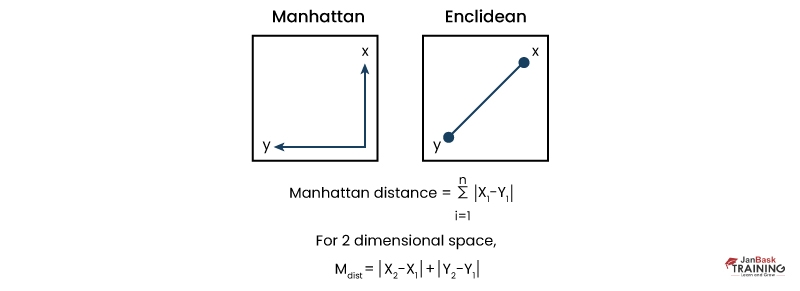
Manhattan distance measure is commonly used in various fields, including computer science, mathematics, and statistics. It is a type of distance metric that measures the difference between two points in space. This measure gets its name from the grid-like structure of Manhattan streets.

The Manhattan distance between two points can be calculated by adding up the absolute differences between their x-coordinates and y-coordinates. For example, suppose we have two points (x1,y1) and (x2,y2). The Manhattan distance between them would be |x1 - x2| + |y1 - y2|. 

This formula can also be extended to higher dimensions as well. For instance, if we have three-dimensional coordinates (x1,y1,z1) and (x2,y2,z2), then the Manhattan distance would be |x1 - x2| + |y1 - y2| + |z1 - z2|. 

One of the advantages of using this metric is that it allows for easy computation since it only involves addition and subtraction operations. Furthermore, because it does not consider diagonal distances or curved paths like other metrics, such as Euclidean Distance Measure, which calculates straight-line distances through space, it tends to produce more accurate results when dealing with city-like grids or street networks.

In real-world applications, this measure finds use in many different areas, such as image processing, where objects must be matched based on their features or characteristics. In logistics management systems where delivery routes are planned along pre-determined road networks, ensuring no detours are taken while optimizing timeframes, etc.

Overall, understanding how to calculate and use the Manhattan Distance Measure can prove highly beneficial, especially when working with data sets containing multiple dimensions such as geographical locations or image feature recognition models.

The Minkowski Distance 

Minkowski distance measure is a mathematical formula that calculates the distance between two points in a multi-dimensional space. It is commonly used in machine learning, data science, and other fields requiring large data analysis.

The Minkowski metric generalizes Euclidean and Manhattan metrics by introducing a parameter p that can take any value greater than zero. When p=1, the Minkowski distance reduces to the Manhattan distance, which measures the absolute differences between coordinates. When p=2, it becomes the Euclidean distance, which measures straight-line distances between points.

However, when p takes on non-integer values or values greater than 2 (e.g., 3/4), it results in what's known as fractional or generalized Minkowski distances. These types of distances are useful for modeling complex phenomena with more nuanced relationships among variables.

For example, you want to classify different types of flowers based on their petal length and width. Using the Minkowski metric with p=2 would measure how far apart each flower is from one other based on their physical characteristics. However, using a fractional value like p=3/4 could capture more subtle differences between flower types that might not be evident using only Euclidean or Manhattan metrics.

One limitation of using fractional or generalized Minkowski distances is that they may not always satisfy certain mathematical properties such as symmetry or triangle inequality. Therefore, choosing an appropriate value for p is important based on your specific application needs and goals.

In summary, the Minkowski distance measure provides a flexible way to calculate distances between points in high-dimensional spaces by allowing for customization through its parameterized form. Its applications range from image recognition to clustering analysis and beyond.

Cosine Similarity 

Cosine similarity is a mathematical concept used to measure the degree of similarity between two vectors in n-dimensional space. It can be applied to any vector data, including text documents, images, and audio files.In the context of text mining and information retrieval tasks, cosine similarity is often used to determine how closely related two documents are based on their contents. In this case, each document is represented as a vector, where each dimension corresponds to a term or word in the document's vocabulary. The value of each dimension represents the frequency or weight of that term in the document.

To calculate cosine similarity between two documents, we first compute their respective vectors using some weighting scheme such as Term Frequency-Inverse Document Frequency (TF-IDF). Then we take the dot product of these vectors and divide it by the product of their magnitudes. The resulting value ranges from -1 (completely opposite) to 1 (identical), with values closer to 1 indicating higher degrees of similarity.Cosine similarity is a powerful tool for comparing and analyzing data represented as vectors in n-dimensional space. It has numerous applications in machine learning, natural language processing, and information retrieval tasks where measuring the similarity between objects or texts is important for making decisions or recommendations.

Jaccard Similarity 

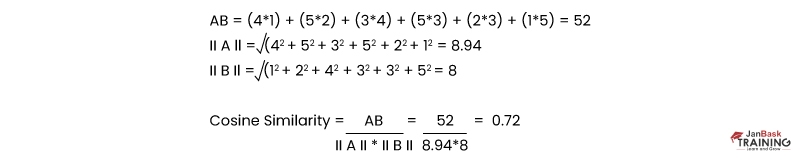
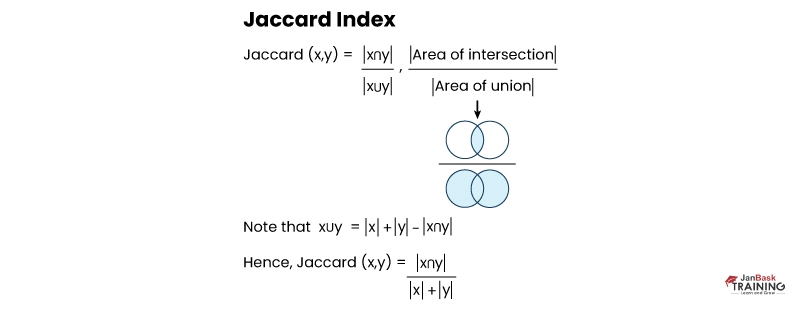
Jaccard Similarity is a widely used technique for measuring similarity between two data sets. It is particularly useful when dealing with categorical variables, where the data can be classified into discrete groups or categories. In essence, Jaccard similarity calculates the overlap between two sets by dividing their intersection by their union.

To illustrate this concept, let us consider an example of two sets,2 A and B: 

A = {apple, banana, orange} 

B = {banana, grapefruit}

The intersection of these two sets contains only one element - "banana". The union of these two sets contains four elements - "apple", "banana", "orange," and "grapefruit". Therefore, the Jaccard similarity coefficient between A and B is 1/4 or 0.25.

This coefficient ranges from 0 (no overlap) to 1 (complete overlap). If the coefficient is closer to 1, then it indicates that there are more common elements in both sets, which means they are more similar to each other.

Jaccard similarity has many applications in various fields, such as information retrieval systems like search engines, where it helps to identify relevant documents based on keywords entered by users. It also plays a significant role in machine learning algorithms like clustering and recommendation systems that rely on identifying similarities between different datasets.Jaccard Similarity provides a simple yet effective way to measure the degree of association between any given pair of categorical variables. By comparing the ratio of shared items within each set relative to its overall size, we can determine how closely related these variables may be. This method can provide valuable insights for researchers across many different industries who need accurate measurements for their data analysis needs.

Different Types of Distance Measures in Clustering

In clustering, different types of distance measures are used depending on the nature of the data and the problem at hand. Some popular distance metrics include:

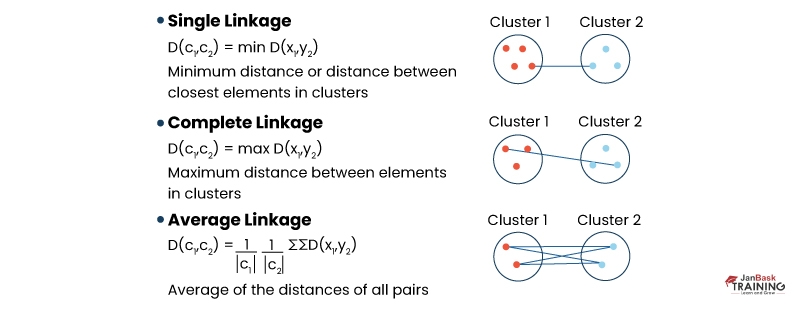
Single Linkage

Single linkage or nearest neighbor clustering uses the minimum distance between any two points in each cluster as a measure for merging clusters together.

Complete Linkage

Complete linkage or farthest neighbor clustering uses maximum distances between any two points in each cluster as a measure for merging clusters together.

Average Linkage

Average linkage computes average distances among all pairs of points from different clusters and merges those with the smallest average distances.

Ward's Method 

Ward's method is a hierarchical clustering algorithm that aims to minimize the variance within each cluster. It works by merging clusters at each step based on their similarity, with the goal of creating clusters that are as internally homogeneous and externally different as possible.

Conclusion

Distance measures are essential in machine learning algorithms, especially regarding unsupervised techniques like clustering. The choice of distance metric depends on various factors such as data type, problem complexity, algorithmic requirements, etc.

In this blog post, we discussed some common types of distance measures used in machine learning, including Euclidean Distance Measure, Manhattan Distance Measure, Minkowski Distance Measure, Cosine Similarity, and Jaccard Similarity, among others. We also explored different types of distance measures used specifically for clusterings, such as single linkage, complete linkage, average linkage, and Ward's method.By understanding these concepts better, you can make more informed decisions about which methods will work best for your specific needs when working with large datasets or complex problems requiring sophisticated analysis tools. Understanding distance measures in algorithm methods begins with understanding data science; you can get an insight into the same through our professional certification and training courses.   

Data Science Training

• Personalized Free Consultation
• Access to Our Learning Management System
• Access to Our Course Curriculum
• Be a Part of Our Free Demo Class

Sign Up Now

FAQ’s

Q.1: What Does a Distance Measure Represent in The Context of Algorithmic Methods and Data Mining?

Ans: In algorithmic methods and data mining, a distance measure is a mathematical technique used to quantify the similarity or dissimilarity between objects or data points. It helps determine the proximity or separation of data points in a dataset.

Q.2: Why are Distance Measures Important in Algorithmic Methods?

Ans: Distance measures are crucial in various algorithmic methods such as clustering, classification, and similarity search. They enable algorithms to measure the similarity between data points, group similar data together, and make decisions based on the calculated distances.

Q.3: What are Some Commonly Used Distance Measures in Data Mining?

Ans: Several distance measures are commonly employed in data mining, including Euclidean distance, Manhattan distance, Cosine similarity, Hamming distance, and Jaccard similarity. Each distance measure has its characteristics and is suitable for different data and analysis tasks.

Q.4: How do Distance Measures Impact the Performance of Clustering Algorithms?

Ans: Distance measures heavily influence the results of clustering algorithms. The choice of distance measure can affect clusters' formation, shape, and interpretation of the clusters. It is essential to select an appropriate distance measure that aligns with the data's characteristics and the clustering task's objectives.

Q.5: Can Different Distance Measures be Combined or Customized for Specific Applications?

Ans: Distance measures can be combined or customized to suit specific applications or data types. Researchers and practitioners often develop domain-specific distance measures that incorporate domain knowledge or adapt existing measures to capture the data's characteristics better. This flexibility allows for more accurate and meaningful analysis in different contexts.