Ultimate Guide to Adaboost Algorithm

Boosting has been a well-liked approach to the resolution of binary classification problems ever since it was first presented in the year 1997. Boosting is a technique that belongs to the ensemble modeling category. This algorithm can modify a group of poor learners into a group of strong learners, considerably expanding the model's prediction ability.The second model is created by using data from the first model via Boosting algorithms, which are then used to improve the deficiencies of the first model. This process is repeated until the dataset can be adequately forecasted and the number of errors has been reduced to an acceptable level.

For the sake of argument, imagine that you trained a decision tree algorithm on the Titanic dataset and that, after doing so, you acquired an accuracy of 80%; this would help demonstrate the idea. KNN can achieve a higher accuracy level than linear regression, which only reaches 70% accuracy, according to the use of a new approach and the verification of its results.The accuracy varies from model to model when the same dataset is used while creating a new model. But instead of using traditional versions of each of these algorithms, we employed hybrid versions to produce our predictions. Our precision will increase if we take the average of the results from these models. Because of this, we can upgrade the accuracy of our projections.Boosting algorithms, in a similar fashion, take input from several models (weak learners) and merge it into a single output (strong learners).

A machine learning method that is part of an Ensemble Approach is called AdaBoost. This technique is also known as Adaptive Boosting. A decision tree with a single split is the AdaBoost algorithm most frequently used in implementations. These are also called Decision Stumps and have a structure similar to a tree.

The model is developed using this strategy, which accords equal significance to each data value. Therefore, points that have been tagged incorrectly are awarded a higher score. The new model offers additional weight to locations with higher importance than the other sites. If a lower error is not obtained during training, the system will continue training until one is received.

Working Process And Need of Adaboost

During the process of boosting, training tuples are each given their own set of weights to lift. k classifiers are learned iteratively. Once a classifier has been discovered, its consequences are modified so that the following classifier, Mi+1, may "pay more attention" to the training tuples that the previous classifier, Mi, missed. The final boosted classifier, denoted by the letter M, considers the votes cast by each classifier. The weight given to each classifier's voice is proportional to the accuracy with which it releases it. A modification of the boosting method called an extension may be used to make predictions about continuous values.

The term "Adaboost" refers to a well-known method of increasing. Consider for a moment that we are interested in enhancing the performance of a specific form of educational strategy. D is a dataset that is made up of d tuples, each of which is labeled with a class (yi). For example, (X1, y1), (X2, y2),..., (Xd, yd) is an example of a tuple pair, and yi refers to the class label of tupleXi. Adaboost begins by assigning a weight of 1/d to each tuple included in the training set. It will take k rounds of the remaining technique before the ensemble will have its full complement of classifiers. In the first round, a training set with the size d is built by picking tuples randomly from the previous set, D. A technique known as "sampling with replacement" allows for many instances of the same tuple to be selected during the sampling process. The likelihood of being chosen from each tuple is directly proportional to the size of that tuple in comparison to the others.

A classifier model called Mi is developed using the training tuples from another model called Di. The next step is to use Di as a test set to evaluate how off it is. In the last step, the weights of the training tuples are adjusted to match the findings of the classification process. If it turns out that a tuple was miscategorized, that tuple will have a heavier weight. If the tuple's categorization was precise, then part of the meaning of the tuple is lost. When trying to classify a tuple, the more challenging it is, the more its weight, and the more frequently it needs to be correctly categorized. The training samples for the classifier used in the subsequent round will be built using these weights. Primarily, we want our freshly made classifier to pay particular attention to the tuples that were erroneously labeled during the previous round of training. Specific classifiers are likely superior to others when assigning labels to distinct "difficult" tuples. These classifiers work together to create a robust system. The method is depicted in Figure 6.32, a visual representation of the algorithm.

Let's take a peek at the math that the algorithm relies on to function. Model The rate of misclassification errors that Mi has is determined by adding up the values of all of the tuples in Di for which Mi has given the incorrect classification. To put that another way,

the error in tuple Xj's mislabeling is represented by err (Xj). If the tuple were mislabeled, the err(Xj) value would be 1 in this scenario. In such a case, it would be equal to 0. When the performance of the classifier Mi falls below a 0.5 error threshold, we will no longer utilize it. Instead, we will begin from scratch by putting up an entirely new Di training set and then use it to infer a wholly new Mi.The rate of Mi's error determines how the weights of the training tuples are modified. If the tuple from round I was categorized correctly; then its weight is increased by error(Mi) divided by (1 error(Mi)).

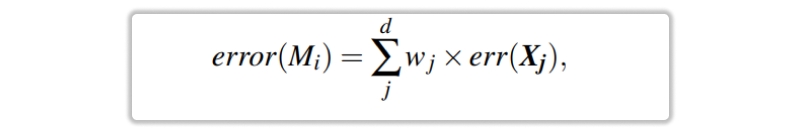
The weights of all tuples (including the misclassified ones) are normalized such that their sum remains constant from before as soon as the weights of the correct categorized tuples have been updated. To normalize a weight, we multiply it by the sum of the weights from the iteration before this one, then divide that outcome by the total number of weights used in this iteration. As a result, the weights of misclassified tuples are increased while the weights of tuples that have been correctly classified are decreased.Once boosting has been done, the question that has to be answered is, "How is the ensemble of classifiers used to forecast the class label of a tuple, X?" However, even though bagging ensured that each classifier received the same number of votes,

A weight is given to each classifier's vote in boosting, which is determined by how well the classifier performed. If a classifier has a low error rate, it has a high level of accuracy; hence, its weight in the voting process ought to increase. The magnitude of the classifier's weight Mi 's vote is

Standard Steps To Explain Adaboost

How Does Adaboost Work?

To understand how Adaboost works, let's look at its steps:

Step 1: Initialize instance weights

In the first iteration of the algorithm, all cases are given equal weight (i.e., w_i = 1/n).

Step 2: Train Weak Classifier

A weak classifier h_t(x) is trained on the dataset using instance weights w_i.

Step 3: Calculate the Error Rate

The error rate e_t of h_t(x) over all instances i=1,...n is calculated as follows:

e_t = sum(w_i * I(y_i != h_t(x_i))) / sum(w_i)

Where y_i is the true label of instance i, and I() is an indicator function that returns 1 if its argument is valid and 0 otherwise.

Step 4: Calculate Classifier Weight

The weight alpha_t of h_t(x) in the final model is calculated as follows:

alpha_t = log((1 - e_t) / e_t)

This weight measures how well the weak classifier performed. It will have a higher weight in the final model if it has high accuracy (low error rate).

Step 5: Update Instance Weights

The weights w_i are updated based on whether each instance was correctly or incorrectly classified by h_t(x):

w_i = w_i * exp(alpha_t * I(y_i != h_t(x)))

Instances that were misclassified by h_t(x) get higher weights, while those that were correctly classified get lower weights. This ensures that Adaboost focuses on difficult instances during training.

Step 6: Normalize Weights

Finally, all instance weights are normalized so they sum up to one:

w_1,...,w_n = w_1,...,w_n / sum(w_1,...,w_n)

Advantages 

AdaBoost's many benefits include its clarity and the need for less tinkering with settings than other algorithms. Moreover, AdaBoost may be used with SVM for added effectiveness. Despite the lack of empirical evidence, AdaBoost is not susceptible to overfitting in theory. One possible explanation is that the learning process is sluggish because parameters are not collaboratively tuned. Read this website if you want to learn the math in detail.AdaBoost's adaptability comes from the fact that it may be used to fortify less-than-perfect classifiers. These days, it's not just used for binary classification but also text and picture categorization. Learn in detail all about the adaboost classifier, adaboost sklearn and adaboost algorithm to understand it better for further utilization.

Several Drawbacks of AdaBoost Include:

Since the boosting method acquires knowledge incrementally, it is crucial to start with accurate information. If you want to utilize AdaBoost, you should know that it is susceptible to noisy data and outliers; therefore, cleaning up your data is necessary.It has also been demonstrated that AdaBoost is less efficient than XGBoost.

Applications of Adaboost

Adaboost has been successfully applied to various machine-learning problems, such as:

• Face detection: Adaboost-based object detectors have been used for face detection in images and videos.
• Fraud detection: Adaboost can detect fraudulent transactions in financial data.
• Medical diagnosis: Adaboost can help diagnose diseases based on medical records and symptoms.
• Natural language processing (NLP): Adaboost has been used for sentiment analysis and text classification tasks in NLP.
• Adaboost's ability to combine multiple weak classifiers into a strong one makes it powerful. 

Data Science Training For Administrators & Developers

• No cost for a Demo Class
• Industry Expert as your Trainer
• Available as per your schedule
• Customer Support Available

Enroll for Demo Class

Conclusion

Adaboost is a powerful boosting algorithm that can significantly improve the accuracy of machine-learning models. By combining multiple weak classifiers, it creates a strong classifier that can accurately classify new instances. Adaboost has been successfully applied to various machine-learning problems such as face detection, fraud detection, medical diagnosis, and NLP. Understanding how Adaboost works and its applications can help data scientists build more accurate business models.You can always take an online course to learn more about Python adaboost, adaboost classifier sklearn, adaboost vs. gradient boosting and adaboost regressor.