Linear Algebra Interview Questions and Answers for Beginners and Advanced

Introduction

Linear algebra is the building block of data science which helps in organizing and understanding data better. For beginners, learning linear algebra is the key to opening doors to data science as it helps in grasping basic ideas like playing with numbers in tables and figuring out patterns in data. For professionals, mastering linear algebra can help them work faster with big data, build smarter models, and make better decisions. 

Today’s linear algebra questions and answers will help you learn and practice for your data science interview and enhance your data science journey!

Q1: Why Is Linear Algebra An Important Part Of Data Science?

A: Linear ALgebra is an important part of data science as it regulates how matrices work, and matrices are everywhere. Matrix representations of important objects include:

• Data: The most generally useful representation of numerical data sets are as n × m matrices. The n rows represent objects, items, or instances, while the m columns each represent distinct features or dimensions.

• Geometric point sets: An n×m matrix can represent a cloud of points in space. The n rows each represent a geometric point, while the m columns define the dimensions. Certain matrix operations have distinct geometric interpretations, enabling us to generalize the two-dimensional geometry we can actually visualize into higher-dimensional spaces.

Q2: What Are Effective Strategies For Solving Problems Involving Large Matrices?

A: There's no one definitive approach as the best strategy for solving problems with large matrices varies based on the specific scenario. Nonetheless, some general strategies include breaking down the problem into smaller parts, utilizing numerical methods for approximations, and employing matrix decomposition techniques to simplify the matrix.

Q3: Why Is Understanding The Dimensionality Of A Matrix Crucial In Vector Operations?

A: Understanding the dimensionality of a matrix is an important part in vector operations because it defines the matrix's number of rows and columns. This information is essential to perform operations accurately. 

For example, when multiplying matrices, the number of columns in the first matrix must match the number of rows in the second matrix for the operation to be valid. Incorrect dimensions would render the operation impossible.

Q4: How Can We Tackle Problems Involving Large Matrices Effectively?

Solving problems with large matrices doesn't have a one-size-fits-all solution. It depends on the specific problem. However, some helpful tips include breaking the problem into smaller parts, using numerical methods for approximations, and simplifying matrices using techniques like decomposition

Q5: What's The Simplest Way To Grasp Linear Transformations?

A: Visualizing linear transformations is easiest when you think of them as changing the basis. When you apply a linear transformation T to a vector v, you get T(v), representing v's shift from the original basis to the new one defined by T. This is why we often represent linear transformations with matrices—they define a new basis.

Q6: How Is Linear Algebra Used In Computer Science?

A: In computer science, linear algebra plays various roles like solving linear equations, manipulating matrices, and transforming vectors. It's also vital in fields like machine learning and artificial intelligence for tasks such as training neural networks and performing matrix operations.

Q7: What Is The Process Of Adding Or Subtracting Vectors?

A: Adding or subtracting vectors involves combining them together to create a new vector. The process remains the same whether you're adding or subtracting; you combine the vectors component-wise. For instance, if you have vectors A and B, and you want to add them to form a new vector C, you'd execute:

C = A + B

This creates a new vector where each component is the sum or difference of the corresponding components of A and B.

Q8: Why Do We Need To Know The Dimensions Of Matrices When Solving Systems Of Linear Equations?

A: Understanding the dimensions of matrices is crucial because they determine the possible solutions to the system of equations. If the matrices are different sizes, there won't be any solutions. If they are the same size, the system can have one solution, no solutions, or infinitely many solutions

Q9: How Do You Define A Linear Equation?

A: A linear equation is defined by the sum of variables weighted by constant coefficients, like:

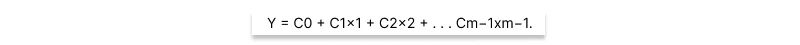
A system of n linear equations can be represented as an n × m matrix, where each row represents an equation, and each of the m columns is associated with the coefficients of a particular variable (or the constant “variable” 1 in the case of c0). Often it is necessary to represent the y value for each equation as well. This is typically done using a separate n × 1 array or vector of solution values.

Q10: What Is The Importance Of Associativity In Linear Algebra?

A: There are two primary reasons why associativity matters to us. In an algebraic sense, it enables us to identify neighboring pairs of matrices in a chain and replace them according to an identity, if we have one. But the other issue is computational. The size of intermediate matrix products can easily blow up in the middle. 

Suppose we seek to calculate ABCD, where A is 1×n, B and C are n×n, and D is n×1. The product (AB)(CD) costs only 2n2 =n operations, assuming the conventional nested-loop matrix multiplication algorithm. In contrast, (A(BC))D weighs in at n3 + n2 + n operations.

Linear algebra interview questions and answers for advanced

Q11: What Is The Significance Of Multiplying Square Matrices By Themselves And Computing Their Powers?

A: Multiplying a square matrix by itself, denoted as A^2 = A × A, is referred to as the square of matrix A, and more generally, A^k is termed the kth power of the matrix. This operation holds significant meaning, particularly in contexts where A represents the adjacency matrix of a graph or network. 

In an adjacency matrix, where A[i, j] = 1 when (i, j) is an edge in the network and 0 otherwise, the product A^2 yields the number of paths of length two in A. Specifically, A^2[i, j] can be computed as the summation of the product of A[i, k] and A[k, j] for all intermediate vertices k, indicating the existence of paths of length two from vertex i to vertex j through intermediate vertices. 

This concept holds relevance not only for 0/1 matrices but also for more general matrices, simulating diffusion effects and iterative processes such as Google's PageRank algorithm and contagion spreading.

Q12: Explain Graphs And Rearrangement Operations In Linear Algebra.

A: Graphs are made up of vertices and edges, where edges are defined as ordered pairs of vertices, like (i, j). A graph with n vertices and m edges can be represented as an n × n matrix M, where M [i, j] denotes the number (or weight) of edges from vertex i to vertex j. There are surprising connections between combinatorial properties and linear algebra, such as the relationship between paths in graphs and matrix multiplication, and how vertex clusters relate to the eigenvalues/vectors of appropriate matrices.

Whereas rearrangement operations can do things. Carefully designed matrices can perform geometric operations on point sets, like translation, rotation, and scaling. Multiplying a data matrix by an appropriate permutation matrix will reorder its rows and columns. Movements can be defined by vectors, the n × 1 matrices powerful enough to encode operations like translation and permutation.

Q13: Give A Brief Overview Of Factoring Matrices.

A: Factoring matrix A into matrices B and C represents a particular aspect of division. We have seen that any non-singular matrix M has an inverse M−1, so the identity matrix I can be factored as I = MM−1. This proves that some matrices (like I) can be factored, and further that they might have many distinct factorizations. In this case, every possible non-singular M defines a different factorization.

Matrix factorization is an important abstraction in data science, leading to concise feature representations and ideas like topic modeling. It plays an important part in solving linear systems, through special factorizations like LU-decomposition.

Unfortunately, finding such factorizations is problematic. Factoring integers is a hard problem, although that complexity goes away when you are allowed floating point numbers. Factoring matrices proves harder: for a particular matrix, exact factorization may not be possible, particularly if we seek the factorization M = XY where X and Y have prescribed dimensions.

Q14: What Is LU Decomposition?

A: LU decomposition is a particular matrix factorization which factors a square matrix A into lower and upper triangular matrices L and U, such that A = L·U. 

A matrix is triangular if it contains all zero terms either above or below the main diagonal. The lower triangular matrix L has all non-zero terms below the main diagonal. The other factor, U, is the upper triangular matrix. Since the main diagonal of L consists of all ones, we can pack the entire decomposition into the same space as the original n × n matrix.

The primary value of LU decomposition is that it proves useful in solving linear systems AX = Y , particularly when solving multiple problems with the same A but different Y . The matrix L is what results from clearing out all of the values above the main diagonal, via Gaussian elimination. 

Once in this triangular form, the remaining equations can be directly simplified. The matrix U reflects what row operations have occurred in the course of building L. Simplifying U and applying L to Y requires less work than solving A from scratch.

Q15: What Are Eigenvector–Eigenvalue Pairs?

A:  Multiplying a vector U by a square matrix A can have the same effect as multiplying it by a scalar l. Consider this pair of examples. Indeed, check them out by hand:

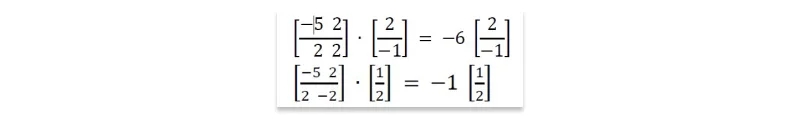
Both of these equalities feature products with the same 2 × 1 vector U on the left as on the right. On one side U is multiplied by a matrix A, and on the other by a scalar λ. In cases like this, when AU = λU, we say that λ is an eigenvalue of matrix A, and U is its associated eigenvector.

Such eigenvector–eigenvalue pairs are a curious thing. That the scalar λ can do the same thing to U as the entire matrix A tells us that they must be special. Together, the eigenvector U and eigenvalue λ must encode a lot of information about A.

Further, there are generally multiple such eigenvector–eigenvalue pairs for any matrix. Note that the second example above works on the same matrix A, but yields a different U and λ.

Q16: What Is The Definition Of The Rotation Matrix R? In Two Dimensions, And How Is It Applied To Rotate Points About The Origin?

A: The rotation matrix Rθ in two dimensions, performing the transformation of rotating points about the origin through an angle of θ, is defined as:

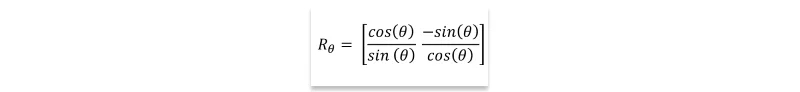
When applied to a point (x, y), the rotation is achieved by multiplying it by the rotation matrix Rθ:

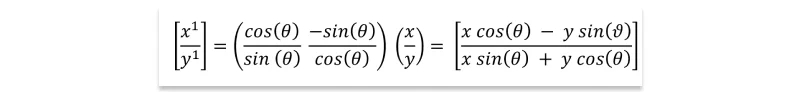
For θ = 180° = π radians, where cos(θ) = -1 and sin(θ) = 0, the rotation matrix yields (-x, -y), effectively placing the point in the opposing quadrant.

To extend this transformation to an (n×2)-dimensional point matrix S, the transpose function can be used to orient the matrix correctly. The expression:

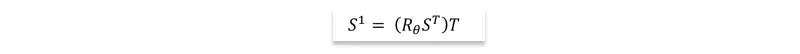
confirms that the operation of rotating the points exactly as intended. Moreover, natural generalizations of Rθ exist to rotate points in arbitrary dimensions. Successive transformations involving rotations, dilations, and reflections can be realized by multiplying chains of rotation, dilation, and reflection matrices. This approach offers a compact description of complex manipulations.

Q17: What Are The Properties Of Eigenvalues?

A: The theory of eigenvalues gets us deeper into the thicket of linear algebra generally speaking, however, we can summarize the properties that will prove important to us:

• Each eigenvalue has an associated eigenvector. They always come in pairs.

• There are, in general, n eigenvector–eigenvalue pairs for every full rank n × n matrix. 

• Every pair of eigenvectors of a symmetric matrix are mutually orthogonal, the same way that the x and y-axes in the plane are orthogonal. Two Vectors are orthogonal if their dot product is zero. Observe that (0, 1) · (1, 0) = 0, as does (2, −1) · (1, 2) = 0 from the previous example.

• The upshot from this is that eigenvectors can play the role of dimensions or bases in some n-dimensional space. This opens up many geometric interpretations of matrices. In particular, any matrix can be encoded where each eigenvalue represents the magnitude of its associated eigenvector.

Q18: How Can One Reduce The Dimensionality Of Data Sets With Principal Components Analysis?

A: Principal components analysis (PCA) is a closely related technique for reducing the dimensionality of data sets. Like SVD, we will define vectors to represent the data set. Like SVD, we will order them by successive importance, so we can reconstruct an approximate representation using few components. PCA and SVD are so closely related as to be indistinguishable for our purposes. They do the same thing in the same way, but coming from different directions.

The principal components define the axes of an ellipsoid best fitting the points. The origin of this set of axes is the centroid of the points. PCA starts by identifying the direction to project the points on to so as to explain the maximum amount of variance. 

This is the line through the centroid that, in some sense, best fits the points, making it analogous to linear regression. We can then project each point onto this line, with this point of intersection defining a particular position on the line relative to the centroid.

Q19: What Decomposition Method Can Be Used For Any N × N Symmetric Matrix, And How Is It Represented Mathematically?

A: Any n × n symmetric matrix M can be decomposed into the sum of its n eigenvector products. This decomposition utilizes the eigenpairs (λi, Ui), sorted by size such that λi ≥ λi−1 for all i. Each eigenvector Ui, being an n × 1 matrix, is multiplied by its transpose (UiUi^T), resulting in an n × n matrix product. The linear combination of these matrices, weighted by their corresponding eigenvalues, reconstructs the original matrix M, as expressed by the equation:

                                                  

This decomposition method is applicable only to symmetric matrices. However, covariance matrices are always symmetric, making them suitable for this decomposition approach. Representing a covariance matrix through its eigenvalue decomposition requires slightly more space than the initial matrix, involving n eigenvectors of length n and n eigenvalues compared to the n(n + 1)/2 elements in the upper triangle of the symmetric matrix plus the main diagonal.

Q20: What Are Some Important Properties Of Matrix Multiplication?

A: The most important properties of matrix multiplication are:

• It does not commute: Commutativity is the notation that order doesn’t matter, that x · y = y · x. Although we take commutativity for granted when multiplying integers, order does matter in matrix multiplication. For any pair of non-square matrices A and B, at most one of either AB or BA has compatible dimensions. But even square matrix multiplication does not commute, as shown by the products below:

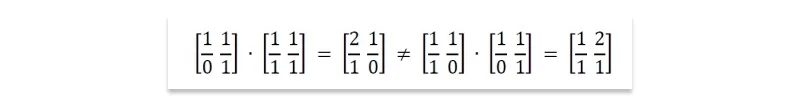
• Matrix multiplication is associative: Associativity grants us the right to parenthesize as we wish, performing operations in the relative order that we choose. In computing the product ABC, we have a choice of two options: (AB)C or A(BC). Longer chains of matrices permit even more freedom, with the number of possible parenthesizations growing exponentially in the length of the chain. All of these will return the same answer, as demonstrated here:

 

Conclusion

If you're looking to up your game, JanBask Training's data science courses can be a game-changer for you. Our structured curriculum and hands-on approach make learning linear algebra and other essential data science skills a breeze. Plus, you'll get expert guidance and practical experience that will boost your confidence and help you excel in the field.